No, Fermat's work is about positive numbers, while this asks about integers, hence it's possible to have negative solutions. Or maybe not. I'm not that into maths to even attempt solving it.Dijkstra said:Fermat's Last Theorem, eh? Didn't it get proven at some point? Though IIRC it would not be something I'd understand or expect anyone here to be able to...ViciousTide said:Prove that a^n = b^n + c^n has no nonzero integer solutions for n>2.
Mathematics trick proof.
- Thread starter Eric the Orange
- Start date
Recommended Videos
Proven in 1995 by Sir Andrew Wiles. Yes, he was actually knighted for solving it.ViciousTide said:Prove that a^n = b^n + c^n has no nonzero integer solutions for n>2.
http://en.wikipedia.org/wiki/Wiles%27s_proof_of_Fermat%27s_Last_Theorem
I know I had a thread about it, might not have been the thread Lionsfan was talking about.DoPo said:That was funny, lol! While I haven't seen the thread, I can just imagine how it went...mmm, that would have been...interestingLionsfan said:The Cracked Article [http://www.cracked.com/blog/6-innocent-sounding-topics-that-are-guaranteed-flame-wars/], unfortunately (fortunately?), the actual topic on here got locked. But yeah......that was a nasty discussion, worse than some of the feminism threads
Most of the posts were people saying I had made a mistake saying 0.9 = 1. I know that it's 0.9 recurring = 1 but I couldn't be bothered to write recurring and I thought it was implied what I was referring to ... alas, I overestimated this sites forum goers or my ability to communicate.
Again, that proof is about positive numbers, not integers as a whole. It's the same thing I said immediately before your comment - we have no solution for negative numbers.Bad Jim said:Proven in 1995 by Sir Andrew Wiles. Yes, he was actually knighted for solving it.ViciousTide said:Prove that a^n = b^n + c^n has no nonzero integer solutions for n>2.
http://en.wikipedia.org/wiki/Wiles%27s_proof_of_Fermat%27s_Last_Theorem
Dang, you got it with out even looking at it, you musta seen alto more of these then I have.DoPo said:snip
My Calc 2 teacher used it to prove that 0 people are passing the class so I guess that's why he chose to do it that way.
Not about mnemonics, just questioning the left to right orderexcalipoor said:The alternative solution is wrong, despite what your mnemonics tell you. Multiplication isn't a higher priority than division, neither is addition higher than subtraction.platinawolf said:8/2*(5-1)+1 = ?
*Snip*
- Feb 7, 2011
- 8,802
- 3,383
- 118
- Country
- 'Merica
- Gender
- 3 children in a trench coat
Now here's a real math trick, and one that's practical, because it gives you INFINITE CHOCOLATE:

What is this witchcraft?Dirty Hipsters said:Now here's a real math trick, and one that's practical, because it gives you INFINITE CHOCOLATE:

https://encrypted-tbn1.gstatic.com/images?q=tbn:ANd9GcQ--90UkVVWF0U0Jv9JvrORSCR77MQbpetjic_XhujtYls_0tiw9w
Seriously how the shit does that work?
Oh that seems fun:madwarper said:If you really wanted to use a mathematical sleight of hand to confuse someone, I prefer using the "30th Dollar" story.
There are 3 businessmen on a trip. They decide to stay over night in a hotel, fortunately the only room open is a triple. The men agree to share it and split the cost evenly, which costs $30.
So, how much does each man pay to split the cost evenly? ___
Ok, the men check into the room and get settled. Later on, when the night clerk comes on, he goes over the books and sees that there's currently a discount on triple rooms and the 3 men had been overcharged. The room actually costs $25. He calls over Johnny the Bellhop, gives him 5 $1 bills and tells him to give the men the refund. Now, Johnny the Bellhop is a bit dishonest and knows that 5 doesn't divide into 3 evenly. He takes 2 $1 bills and puts them into his pocket.
So, how much is in Johnny's pocket? ___ How much is in his hand? ___ How much is in the cash register? ___ And that total is? ___
Ok, Johnny arrives at the triple room, knocks at the door, tells them they had been overcharged and gives them the 3 $1 bills as a refund.
So, how much did each man pay originally? ___ How much did each man get back? ___ So, the each men ended up spending? ___ How much did the 3 men end up paying? ___ And, add the $2 in Johnny's pocket, how much is that? ___ Where's the 30th Dollar?
So, how much does each man pay to split the cost evenly? $10
[...]
So, how much is in Johnny's pocket? 2 $1 bills How much is in his hand? 3 $1 bills How much is in the cash register? $25 And that total is? $30
[...]
So, how much did each man pay originally? $10 How much did each man get back? $1 So, the each men ended up spending? $9 How much did the 3 men end up paying? $27 And, add the $2 in Johnny's pocket, how much is that? $29 Where's the 30th Dollar?
They paid $25 to the register and 5 to the bellhop in essence
Easiest to think of it as 2 10's and a 5
5 person gets 3 back, bringing it up to 8
Thats 10,9 and 9 with 2 dollars in the thief's pocket.
The confusion seems to come from the fact that you are breaking the 30 (divisible by 3) into 25 and 5 (not divisible by 3) and glazing over the 25 section of the problem. To be honest I did have to think it through a bit.
Its just a trick. As it moves the blocks extend downwards a bit, making them bigger than when they started.Evil Smurf said:What is this witchcraft?Dirty Hipsters said:Now here's a real math trick, and one that's practical, because it gives you INFINITE CHOCOLATE:

https://encrypted-tbn1.gstatic.com/images?q=tbn:ANd9GcQ--90UkVVWF0U0Jv9JvrORSCR77MQbpetjic_XhujtYls_0tiw9w
Seriously how the shit does that work?
Damn it, I was hoping for another math-war...
Would have made for a nice change of pace, what with all the sexism.
Though now I am working on the ULTIMATE flamewar-topic...
Would have made for a nice change of pace, what with all the sexism.
Though now I am working on the ULTIMATE flamewar-topic...
Ohh i have a proof i really like. It's not really a trick though, more a joke.
Theorem:
Every Positive Number is interesting.
Proof:
1 is the smallest Positive Number and thus very interesting.
Suppose a Non Empty Set of uninteresting Numbers. Since it's a Subset of all Positive Numbers it is well ordered and thus has a smallest Element. This smallest uninteresting Number is of course very interesting, which leads to a contradiction.
Theorem:
Every Positive Number is interesting.
Proof:
1 is the smallest Positive Number and thus very interesting.
Suppose a Non Empty Set of uninteresting Numbers. Since it's a Subset of all Positive Numbers it is well ordered and thus has a smallest Element. This smallest uninteresting Number is of course very interesting, which leads to a contradiction.
Hmm, actually good thinking. It does boil down to Fermat's Last Theorem again. See, I said I'm not into maths that much - it didn't even cross my mind.Dijkstra said:Well assuming n is an integer, if it's even then negative or positive is irrelevant. If it's odd then if all 3 are negative, that cancels out. If one is negative, move it to the other side and we get the exact same problem. If two are negative... well it can't be both b and c since they couldn't add to a positive. If it's a and another then you just move the other to the same side as a and you get the same problem again. So... if n is an integer then the problem for a, b, and c is an integer reduces to the problem that a, b, and c are positive integers.DoPo said:No, Fermat's work is about positive numbers, while this asks about integers, hence it's possible to have negative solutions. Or maybe not. I'm not that into maths to even attempt solving it.Dijkstra said:Fermat's Last Theorem, eh? Didn't it get proven at some point? Though IIRC it would not be something I'd understand or expect anyone here to be able to...ViciousTide said:Prove that a^n = b^n + c^n has no nonzero integer solutions for n>2.
There's also thisEvil Smurf said:Seriously how the shit does that work?
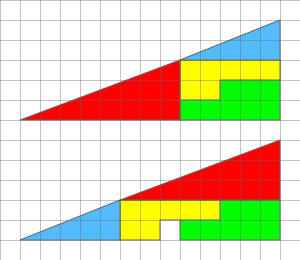
Although I don't know if I was a fan of it. A teacher asked us to 'solve' it, so before doing anything we all said the obvious solution but he actually made us work it out to prove it (and the solution we'd guessed was correct) and it soured me to the puzzle
BrotherRool said:There's also thisEvil Smurf said:Seriously how the shit does that work?

Although I don't know if I was a fan of it. A teacher asked us to 'solve' it, so before doing anything we all said the obvious solution but he actually made us work it out to prove it (and the solution we'd guessed was correct) and it soured me to the puzzle
Yeah, it's not hard to spot that the hypotenuse is not the same across both figures. If you look at the bottom one, you'll see the top corner of the blue triangle meeting the left corner of the red triangle exactly where the square grid intersects. If you look at the same place on the top one (five squares from the left, two from the bottom) you'd notice it's not the same and the side seems to be "pushed in" as opposed to the bottom figure. Same goes for the other meeting point (five from the right, three from the bottom). The hypotenuse is, in fact, NOT, a hypotenuse a really wide angle. Thus changing it around can make a difference, but the figure wasn't a triangle to begin with.
Oh, if we're going for bogus proofs, let's try this. My integral signs look a bit weird, but there's nothing I can do about that.
I =
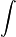 sinh(x) cosh(x) dx
sinh(x) cosh(x) dx
Integrate by parts, where
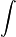 vu' dx = vu -
vu' dx = vu -
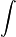 uv' dx
uv' dx
In this case, v = cosh(x) and u' = sinh(x)
This means that v' = sinh(x) and u = cosh(x)
Therefore,
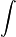 sinh(x) cosh(x) dx = cosh[sup]2[/sup](x) -
sinh(x) cosh(x) dx = cosh[sup]2[/sup](x) -
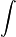 sinh(x) cosh(x) dx
sinh(x) cosh(x) dx
(1): I = cosh[sup]2[/sup](x) - I
Now, take that integral and do it by parts again but with v = sinh(x) and u' = cosh(x), so v' = cosh(x) and u = sinh(x)
Therefore,
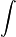 sinh(x) cosh(x) dx = sinh[sup]2[/sup](x) -
sinh(x) cosh(x) dx = sinh[sup]2[/sup](x) -
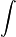 sinh(x) cosh(x) dx
sinh(x) cosh(x) dx
(2): I = sinh[sup]2[/sup](x) - I
(1) - (2): 0 = cosh[sup]2[/sup](x) - I - (sinh[sup]2[/sup](x) - I) = cosh[sup]2[/sup](x) - sinh[sup]2[/sup](x) = 1
Therefore, 0 = 1
I =
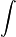
Integrate by parts, where
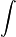
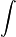
In this case, v = cosh(x) and u' = sinh(x)
This means that v' = sinh(x) and u = cosh(x)
Therefore,
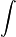
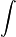
(1): I = cosh[sup]2[/sup](x) - I
Now, take that integral and do it by parts again but with v = sinh(x) and u' = cosh(x), so v' = cosh(x) and u = sinh(x)
Therefore,
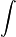
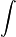
(2): I = sinh[sup]2[/sup](x) - I
(1) - (2): 0 = cosh[sup]2[/sup](x) - I - (sinh[sup]2[/sup](x) - I) = cosh[sup]2[/sup](x) - sinh[sup]2[/sup](x) = 1
Therefore, 0 = 1
